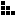 , always produced a line
clear across the narrow dimension of the rectangle, thereby breaking
the 3x44 rectangle into two smaller 3xN rectangles. Looking at the 22
remaining hexominos, I found I could classify them into three
classes:
, always produced a line
clear across the narrow dimension of the rectangle, thereby breaking
the 3x44 rectangle into two smaller 3xN rectangles. Looking at the 22
remaining hexominos, I found I could classify them into three
classes:I've been noodling around with polyominos recently. A friend suggested that some of the results might be worth publishing. I'm not about to write a paper to enrich an already overpriced journal, so I'm writing this blah post instead.
This assumes the reader is familiar with the basic idea of polyominos and a few of their more rudimentary properties. (Particularly likely to be well-known are the pentominos, and, for those who aren't familiar with them but would like to be, the Wikipedia page "Pentomino" is a decent place to start.)
Many years ago, I wrote a program to brute-force such problems. It was not specific to two dimensions, but was specific to the 90-degree cell (square, cube, etc) paradigm—for example, it cannot be used to solve polyhex problems. I then promptly solved numerous pentomino problems with it.
Just recently, as part of a move (still in progress at this writing, sigh), I found something I played with as a kid: a commercial toy (under the name `Multipuzzle') which consisted of a set of hexominos with some duplicates, a 6x10 tray, and a booklet of puzzles. This got me looking at the hexominos.
There are 35 free hexominos. It is thus superfically plausible that they might form any of various rectangles whose sides multiply to 35x6=210, such as 14x15 or 7x30. I threw my program at them. When it hadn't found any solutions to some of the easier-looking problems after a few minutes, I started thinking a bit.
It turns out the 35 hexominos cannot form any of the plausible-looking rectangles. This is easily shown by checkerboard-colouring them. Most of them have three squares of each colour when this is done, but some have a 4/2 split instead of a 3/3 split—and the number of such hexominos is odd. Thus, no shape which has an even split of colour counts when checkerboard-coloured is buildable; since 210 is even, all the relevant rectangles have at least one even side and thus fit this description. (I modified one of them slightly by moving a square to produce a 104/106 split and promptly got a lot of solutions out of my program.)
One of those rectangles the previous paragraph deduces are impossible is the 3x70. Quite aside from the checkerboard colouring, there are some pieces which cannot appear in a 3xN rectangle because, no matter how they are placed, they partition the empty squares into two disconnected sets (because they are at least three squares wide) and leave a non-multiple of 3 vacant cells on each side. If there is such a piece in a 3xN rectangle, the number of cells between it and the rectangle end is not a multiple of 3 and thus not a multiple of 6, so it cannot be filled with hexominos. Thus, none of these pieces can ever be used when building a 3xN rectangle.
Throwing out those pieces leaves 22 hexominos, and now the number of pieces exhibiting the 4/2 checkerboard split is even, so there is no obvious reason a 3x44 rectangle should be impossible. So I sicced my program on that. When it hadn't found any solutions after a while, I started to suspect that it might not be possible.
I also noticed that some pieces, such as 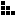 , always produced a line
clear across the narrow dimension of the rectangle, thereby breaking
the 3x44 rectangle into two smaller 3xN rectangles. Looking at the 22
remaining hexominos, I found I could classify them into three
classes:
, always produced a line
clear across the narrow dimension of the rectangle, thereby breaking
the 3x44 rectangle into two smaller 3xN rectangles. Looking at the 22
remaining hexominos, I found I could classify them into three
classes:
There are an odd number (five) class (b) hexominos, but rectangle ends can also be made up from class (a) hexominos, so this doesn't mean much. But any 3x44 solution will be broken up into at least three subrectangles by these pieces. So I looked at it from that point of view.
I built a specialized program which builds 3xN rectangles from the 22 hexominos, stopping as soon as it forms a rectangle. This found 2297151 subrectangles. Then, I threw away the details of each rectangle and considered them just as sets of pieces; any 3x44 solution must be made up of one or more of these sets (two or more, actually, since none were full 3x44 rectangles; three or more, because there are five pieces which force a subrectangle end and thus at least three subrectangles). Looking at it from that point of view reduced the list of 2297151 rectangles down to 24262 sets of pieces. Then I built another program which just took a list of subsets of the 22-element set of pieces and tried to find a set of subsets which were (a) disjoint and (b) covered the whole 22-element set. As a first step, I took each set S and considered the list of `compatible' sets C, sets which had no element in common with S. If the union of S and all the Cs didn't include all 22 pieces, S clearly cannot appear, because there's no way to get the missing piece(s) in. I iterated this until it no longer threw anything out; this left me with 2015 sets. Then I just threw exhaustive search at this: include a set and eliminate all sets that overlap with it; if any sets remain, recurse, otherwise we've found a solution (if all 22 pieces are included) or reached a dead end (if not) and must backtrack.
This completed fairly fast and found no solutions. As a cross-check, I manually constructed some subsets which had solutions (but which didn't correspond to real hexomino rectangles); the program found the solutions just fine.
About this time, the general-purpose exhaustive search program finished working its way through the first rectangle end, without any solutions. Because every solution must be decomposable into rectangles which can then be reordered and rotated, every solution can trivially be transformed to put any desired rectangle end at an end of the 3x44 rectangle, so this means it shouldn't find any solutions at all. I've left it running on the grounds that it will probably finish within a tolerably small number of days, and additional cross-checks are good: solving the same problem twice by drastically different methods gives greater confidence in the solution.
I also got curious about pentomino puzzles. The pentominos add up to 60 squares, and some pentomino puzzle shapes, like the 6x10 rectangle and the 8x8 square with a 2x2 corner cut out, can be seen as a factor-of-2 magnification of a 15-omino. So I generated a list of all 15-ominos (turns out there are 3426576 of them), magnified each one by a factor of 2 (thus quadrupling the square count), and threw them at my solver.
Of the 3426576 resulting pentomino puzzles, most (3326533) have no
solutions. 30134 have only one solution; 23718 have two; 7914 have
three; etc, for a total of 100043 that have solutions. 173 is the
lowest solution count that none of them have. 1261 is the highest
solution count that more than one shape has (the corresponding
15-ominos are 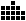 and
and 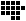 ); the highest five
solution counts are 2910 (
); the highest five
solution counts are 2910 (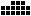 ), 2996 (
), 2996 (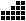 ), 3135 (
), 3135 (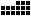 ), 9356 (
), 9356 (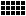 ), and 10054
(
), and 10054
( ). (The last two shapes are
symmetric; the solution counts given are not reduced for their
symmetry, though the last one still has the highest solution count if
they are.)
). (The last two shapes are
symmetric; the solution counts given are not reduced for their
symmetry, though the last one still has the highest solution count if
they are.)
This leads me to wonder what shape has the most solutions. The above run is restricted to shapes formed by magnifying 15-ominos, which is a very restricted subset of the possible 60-ominos. The obvious thing to do is enumerate all 60-ominos and try each one. But there are a quite a lot of them; my rough estimate is somewhere on the order of 1e35, putting even enumerating them well out of reach (mayyyyybe except for the likes of Google or the US's NSA, and even then I'm not sure because it's not obvious to me that the problem parallelizes at all well), with actually doing anything substantial for each one (like running a pentomino-problem solver) utterly hopeless.
I do know that 10054 is not the best possible; I did a few experiments removing three cells from a 7x9 rectangle and found one with over thirteen thousand solutions. (But see EDIT below.)
I'd be interested in any pointers to work on this problem, or any thoughts anyone may have for how to bring it within feasability. So far the best idea I've come up with is to enumerate not 60-ominos but rather ways of forming connected shapes from the pentominos. However, there are an awful lot of those, too, and I'm short of ideas for cutting down the search space.
All the aforementioned programs are available to anyone who wants a copy. I'm keeping them in git repos; the thing to point git clone at, if you want them, is "git://git.rodents-montreal.org/Mouse/pack". If using git is difficult or unpleasant, I can also put things up for anonymous FTP, or even email them.
EDIT, 2022-03-16: the 8x8 square with its four corners removed has
17360 solutions. It would not surprise me if this were the maximum.
(I'm surprised it took me over eight years to think to try this shape.)
Amusingly, if you place the X one cell diagonally in from a corner,
fill the corner with the N, and place the P so as to cover the one
square that simultaneously touches the N, the X, and the edge ( ), then there's only one way to
complete all the rest (
), then there's only one way to
complete all the rest ( )!
)!